+4915150735609

Kurzfassung
Ziel dieser Arbeit war die Entwicklung einer Methode zur Schätzung der wichtigsten Bewegungsgrößen Schwerpunktgeschwindigkeit und Schwimmwinkel (siehe Abbildung 1), um diese einer Fahrdynamikregelung zur Verfügung zu stellen. Dazu sollte lediglich die Sensorik der Electronic Stability Control (ESC) genutzt werden. Damit eine modellbasierte Steuerung oder ein Führungsmodell auf Veränderung des querdynamischen Fahrverhaltens reagieren kann, sollten zusätzlich die fahrdynamisch wichtigsten Parameter, wie die Schräglaufsteifigkeiten und der maximale Reibwert während des Fahrbetriebs geschätzt werden.
Abbildung 1
Fahrdynamische Modelle wurden auf Basis der Starrkörperbewegung im Raum entwickelt, die alle erforderlichen Situationen, wie die Fahrt in der Steilkurve, Fahrten im physikalischen Grenzbereich auf Hoch- und Niedrigreibwert genau genug modellieren. Dabei wurde ein optimaler Kompromiss aus Komplexität und Genauigkeit gefunden. Die fahrzeug- und reifenabhängigen Parameter dieser nichtlinearen Schlupf-Kraftmodelle wurden durch Fahrversuche und einer neu entwickelten Referenzsensorik-Konfiguration bestehend aus 6D-IMU, GPS und Correvit-Sensor identifiziert. Dabei wurden erstmals auch Manöver mit gleichzeitigem Längs- und Querschlupf (Kurvenbremsungen) verwendet, um die Querkraftabschwächung in Abhängigkeit des Längsschlupfes zu parametrieren. Die Validierung mit einer Kurvenbremsung bei maximaler Querbeschleunigung zeigt die Leistungsfähigkeit des resultierenden Fahrdynamikmodells auf, siehe Abbildung 2.
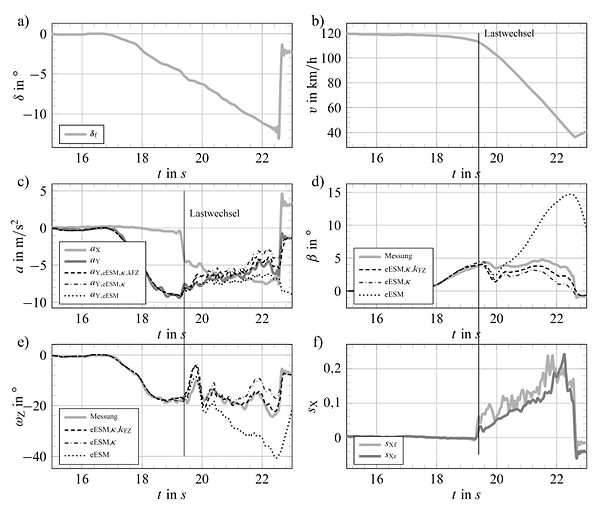
Abbildung 2: Simulation von drei Varianten des nichtlinearen Einspurmodells (eESM) und Vergleich
mit einer Messung; Manöver: Vollbremsung bei maximaler Querbeschleunigung; a)
Lenkwinkel der Vorderachse; b) Geschwindigkeit. c) Längs- und Querbeschleunigung; d)
Schwimmwinkel; e) Gierrate; f) Einspurmodell-Schlupf
Die Schätzung der fahrdynamischen Zustände und Parameter mit ESC-Sensorik wurde auf Basis von erweiterten und Unscented Kalman-Filtern entwickelt. Die Prädiktion der Zustände erfolgte wie in der Luft- und Raumfahrt üblich mit einem kinematischen Modell, d.h. durch Integration der Längs- und Querbeschleunigungsensorsignale, sowie der Gierrate. Die Korrektur dieser instabilen Integration erfolgte durch die Geschwindigkeiten der Vorderräder und mit den (aus Sensorgrößen geschätzten) Längs- und Querkräften der Vorder- und Hinterachse. Durch Berücksichtigung desmaximalen Reibwerts in den Achslängs- und Querkraftmodellen wird dieser bei genügend Schlupfbeobachtbar.
Es konnte gezeigt und erstmals begründet werden, warum der hier zur Zustandsschätzung eingesetzte Unscented Kalman-Filter im fahrdynamischen Grenzbereich durch die Berücksichtigung der Nichtlinearität den Schwimmwinkel robuster als der erweiterte Kalman-Filter schätzt. Die Schwimmwinkelschätzung wurde mittels 355 unterschiedlicher, vom Autor selbst durchgeführter Testfahrten auf Fahrdynamikflächen, Steilkurven, Handlingkursen (siehe Beispiel in Abbildung 3) und auf Schnee validiert. Der Algorithmus lieferte auf ca. 1000 Testfahrt-Kilometern in allen erdenklichen fahrdynamisch relevanten Situationen robuste Ergebnisse. Im Mittel betrug der maximale Schwimmwinkelfehler während einer Testfahrt 2,7 Grad. Der entwickelte Schwimmwinkelschätzer kann daher einen entscheidenden Beitrag bei der Weiterentwicklung des ESC leisten, indem insbesondere kritische Situationen frühzeitig erkannt werden. Die Reibwertschätzung reagierte sehr schnell, sodass bereits bei ca. 80-85% der maximalen Querbeschleunigung der maximale Reibwert richtig eingeschätzt wurde. Die Schräglaufsteifigkeiten konnten während einer Landstraßenfahrt mit mittleren Querbeschleunigungen robust geschätzt werden. Der Unterschied zwischen einer Winter und Sommerbereifung wurde deutlich.
Abbildung 3
Um das Zusammenspiel des entwickelten Schätzalgorithmus mit einer Fahrdynamikregelung zu demonstrieren, wurde eine Modellfolgesteuerung einer aktiven Vorder- und Hinterachslenkung zur Verbesserung der Gierdynamik in einer IPG-Carmaker-Simulation implementiert. Durch die Rückführung des geschätzten Schwimmwinkels und einem einfachen P-Regler konnte das Fahrzeug durch Bremseingriffe auch bei einem langsam anwachsenden Schwimmwinkeln frühzeitig stabilisiert werden, was durch eine Gierratenrückführung nicht möglich war.


Ergebnisse
In dem Video sehen sie mich beim Test des entwickelten Schwimmwinkelschätzers. Das rote Signale ist der Referenzschwimmwinkel des Fahrzeug, gemessen mit einem "Correvit"-Sensor, der auf der Erkennung von Texturverschiebungen mittels 2-phasigen optischen Gittersystemen
basiert. Diese Signal beantwortet die Frage: "Wie quer fahr ich gerade wirklich?" Das blaue Signal ist das Ergebnis des neu entwickelten Schätzers. Bei der Verwendung von Kalmanfiltern fällt auch immer nützliches Nebenprodukt ab, die Kovarianzmatrix. Die Diagonalelemente geben Auskunft in welchem Bereich der aktuelle Schätzfehler voraussichtlich liegen wird (türkisfarbige Signale). Immer wenn das System nicht beobachtbar ist, wird dieser Bereich größer (Fahren am querdynamischen Limit), da nur noch die Signale der Inertialeinheit aufintegriert werden. Immer dann, wenn der Fahrer beim Drift wieder gegenlenkt und der Schräglaufwinkel an der Vorderachse klein wird, wird der Schwimmwinkel über das Reifenmodell wieder beobachtbar und der mögliche Fehlerbereich wird wieder kleiner. Im nächsten Abschnitt wird dieser Zusammenhang in einer Grafik näher erklärt.

Unscented Kalmanfilter, Sigma-Points und Driften
In der Grafik sehen Sie a) die geschätzten Querkräfte der Vorder- und Hinterachse normiert auf die Radlast, b) die geschätzten und wahren Schräglaufwinkel der Vorder- und Hinterachse und c) einen ausgewählten Arbeitspunkt bei dem die aktuell verwendeten Reifenkennlinien dargestellt sind. Die Vorderachse hat einen Schräglaufwinkel bei dem noch ein deutlicher Zusammenhang zwischen Schräglaufwinkel (direkter Zusammenhang mit dem Schwimmwinkel) und Querkraft besteht. Dieser Zusammenhang wird bei einem Unscented Kalmanfilter durch das streuen von sogenannten "Sigma-Points" durch das nichtlineare System erfasst (rote Punkte). Der Schwimmwinkel lässt sich demnach mit der Vorderachse noch gut beobachten. Der Unscented Kalmanfilter stellt dementsprechend eine Rückführverstärkung größer Null für die Vorderachsquerkraft ein.
Die Hinterachse, hat im aktuellen Arbeitspunkt sehr viel Schlupf und Schräglaufwinkel, sodass die Reifenkennlinie sehr flach wird und kaum noch ein Zusammenhang zwischen Schwimmwinkel und Querkraft besteht. Dementsprechend wird die Rückführverstärkung auf den Schwimmwinkel nahe Null. Allerdings kann jetzt mit der Hinterachsquerkraft der maximale Reibwert beobachtet werden!
Dies war nur eine sehr flüchtige Erklärung für ein sehr schwierig zu verstehendes und hoch nichtlineares Problem. Bei weiteren Fragen kontaktieren sie mich einfach.
